La matrice di incidenza in un grafo
La matrice di incidenza di un grafo è una matrice che rappresenta la relazione tra i vertici e i grafi dove le righe rappresentano i vertici e le colonne rappresentano gli spigoli.
E' un'altra forma di rappresentazione matematica di un grafo, sia esso diretto (digrafo) o non diretto.
Grafi semplici
In un grafo non direzionato, la matrice di incidenza è una matrice \( n \times m \), dove \( n \) è il numero di vertici \( m \) è il numero di spigoli
Ogni colonna della matrice rappresenta uno spigolo del grafo, e ogni riga rappresenta un vertice.
Gli elementi della matrice sono marcati con
- 1 se il vertice corrispondente alla riga è un estremo dello spigolo corrispondente alla colonna
- 0 se il vertice corrispondente alla riga non è un estremo dello spigolo corrispondente alla colonna
A differenza della matrice di adiacenza che si focalizza sui rapporti tra vertici, la matrice di incidenza mostra la relazione tra vertici e spigoli.
Esempio
Consideriamo un grafo con 4 vertici \( A, B, C, D \) e 4 spigoli \( e_1, e_2, e_3, e_4 \).
Dove \( e_1 \) collega \( A \) a \( B \), \( e_2 \) collega \( B \) a \( C \), \( e_3 \) collega \( C \) a \( D \), e \( e_4 \) collega \( D \) a \( A \).
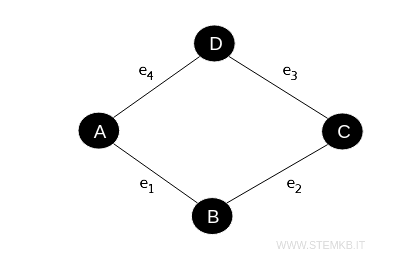
Possiamo rappresentare la matrice di incidenza come segue.
\[
\begin{array}{c|cccc}
& e_1 & e_2 & e_3 & e_4 \\
\hline
A & 1 & 0 & 0 & 1 \\
B & 1 & 1 & 0 & 0 \\
C & 0 & 1 & 1 & 0 \\
D & 0 & 0 & 1 & 1 \\
\end{array}
\]
Ogni colonna rappresenta uno spigolo, e ogni riga rappresenta un vertice.
Il valore "1" indica che il vertice corrispondente è collegato da quel particolare spigolo.
Viceversa, il valore "0" significa che il vertice non è collegato allo spigolo.
Grafi diretti
Per i digrafi, la matrice di incidenza si adatta per riflettere la direzione degli spigoli.
In questo caso le righe rappresentano i vertici (nodi) mentre le colonne rappresentano gli spigoli (archi).
Gli elementi della matrice possono essere
- -1 se il vertice corrispondente alla riga è l'estremo iniziale dell'arco corrispondente alla colonna
- 1 se il vertice corrispondente alla riga è l'estremo finale dell'arco corrispondente alla colonna
- 0 se il vertice corrispondente alla riga non è un estremo dell'arco corrispondente alla colonna
Questa rappresentazione offre un modo diretto per visualizzare e manipolare le relazioni spigolo-vertice nei grafi, essendo particolarmente adatta per questioni di connettività e percorrenza.
Nella matrice di incidenza di un digrafo la somma di ogni colonna è nulla, perché ogni arco ha sempre una coda (vertice di origine) e una testa (vertice di destinazione).
Esempio
Prendiamo come esempio un digrafo con 4 vertici e 4 archi direzionati \( e_1, e_2, e_3, e_4 \).
Dove \( e_1 \) va da \( A \) a \( B \), \( e_2 \) va da \( B \) a \( C \), \( e_3 \) va da \( C \) a \( D \), e \( e_4 \) va \( D \) ad \( A \).
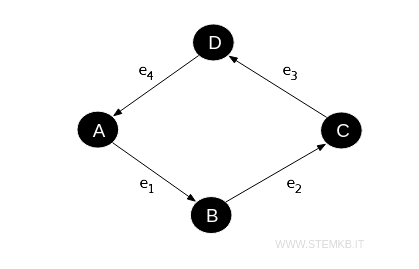
In questo caso la matrice di incidenza sarebbe:
\[
\begin{array}{c|cccc}
& e_1 & e_2 & e_3 & e_4 \\
\hline
A & -1 & 0 & 0 & 1 \\
B & 1 & -1 & 0 & 0 \\
C & 0 & 1 & -1 & 0 \\
D & 0 & 0 & 1 & -1 \\
\end{array}
\]
Ogni riga rappresenta un nodo (vertice) mentre ogni colonna rappresenta un arco del digrafo.
Nella matrice:
- -1 indica che il vertice è l'origine dell'arco
- 1 indica che il vertice è la destinazione dell'arco
- 0 indica che il vertice non è connesso dall'arco
Alcune rappresentazioni potrebbero utilizzare differenti convenzioni per indicare la direzione degli archi, o la presenza di cappi nei digrafi, a seconda del contesto o del software utilizzato.
La matrice di incidenza è particolarmente utile per analizzare la struttura dei grafi e dei digrafi in termini di connessioni tra vertici e spigoli.