La proporzionalità diretta
Cosa significa proporzionalità diretta?
Due grandezze \( x \) e \( y \) sono direttamente proporzionali quando il loro rapporto è costante. In termini matematici, questo si esprime con: $$ \frac{y}{x} = k \quad \text{oppure} \quad y = kx $$ dove \( k \) è una costante chiamata coefficiente di proporzionalità.
La proporzionalità diretta è una delle relazioni matematiche più semplici e fondamentali che possono esistere tra due grandezze.
Questo tipo di relazione è ampiamente utilizzato nella fisica e in molte altre discipline per descrivere fenomeni in cui due variabili crescono o decrescono insieme mantenendo un rapporto costante.
Le caratteristiche principali della proporzionalità diretta sono:
- Costanza del rapporto: Qualunque siano i valori di \( x \) e \( y \), il rapporto \( \frac{y}{x} \) resta invariato.
- Incremento proporzionale: Se \( x \) raddoppia, triplica o quadruplica, anche \( y \) raddoppia, triplica o quadruplica.
- Grafico lineare: La rappresentazione grafica della relazione è una retta che passa per l’origine (\( 0,0 \)), con inclinazione determinata dal valore di \( k \).
Un esempio pratico
Immaginiamo di voler analizzare la relazione tra il volume di benzina acquistato e il relativo prezzo.
Se il prezzo unitario della benzina è \( 1,50 \, \text{€/L} \), i dati raccolti potrebbero essere:
| Volume (\( x \), in L) | Prezzo (\( y \), in €) |
|---|---|
| 1,00 | 1,50 |
| 2,00 | 3,00 |
| 3,00 | 4,50 |
| 4,00 | 6,00 |
Osservando la tabella, calcoliamo il rapporto \( \frac{y}{x} \) per ogni coppia di valori:
$$ \frac{1,50}{1,00} = 1,50, \quad \frac{3,00}{2,00} = 1,50, \quad \frac{4,50}{3,00} = 1,50, \quad \frac{6,00}{4,00} = 1,50 $$
Come si può vedere il rapporto è costante e rappresenta il prezzo unitario della benzina (\( k = 1,50 \)).
La relazione tra \( y \) (prezzo) e \( x \) (volume) può essere espressa con la funzione:
$$ y = 1,50x. $$
Ora rappresentiamo questa funzione su un diagramma cartesiano.
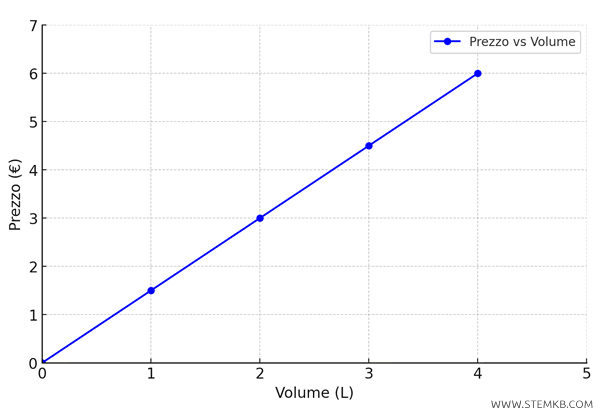
Il grafico descrive una retta che passa per l’origine (\( 0,0 \)), poiché senza acquistare benzina (\( x = 0 \)) non si spende nulla (\( y = 0 \)), e ha l'inclinazione determinata dal coefficiente \( k = 1,50 \), che rappresenta il prezzo per litro.
Supponiamo che il prezzo della benzina aumenti a \( 1,90 \, \text{€/L} \). La nuova equazione sarà:
$$ y = 1,90x $$
In un grafico, questa retta avrà una pendenza maggiore, indicando un costo unitario più elevato.
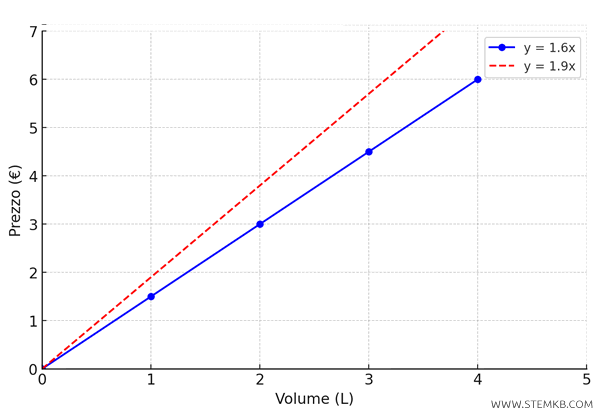
Ogni variazione di \( k \) implica una modifica nella relazione tra \( x \) e \( y \) che è visibile graficamente nella pendenza della funzione.
In generale, la pendenza della retta dipende dal valore di \( k \):
- Maggiore è \( k \), più ripida è la retta.
- Minore è \( k \), più piatta è la retta.
Oltre agli esempi quotidiani come il costo della benzina, questa relazione descrive fenomeni fisici fondamentali, come la velocità costante in un moto rettilineo uniforme (\( s = vt \)) e la legge di Hooke per le molle (\( F = kx \)).