La proporzionalità inversa
Cos’è la proporzionalità inversa?
La proporzionalità inversa descrive una relazione tra due quantità in cui una aumenta mentre l’altra diminuisce, in modo che il loro prodotto rimanga costante. $$ x \cdot y = k $$ Dove \(x\) e \(y\) sono le due variabili, \(k\) è una costante positiva.
Per esempio, se \(k = 100\), allora le possibili coppie di valori per \(x\) e \(y\) che soddisfano questa equazione sono:
- \(x = 1, y = 100\)
- \(x = 2, y = 50\)
- \(x = 4, y = 25\)
Questa relazione è detta “inversa” perché, all’aumentare di una variabile, l’altra diminuisce proporzionalmente.
Proviamo a mettere in tabella alcuni numeri che soddisfano questa relazione.
| x | y (k / x) |
|---|---|
| 1 | 100.0 |
| 2 | 50.0 |
| 4 | 25.0 |
| 5 | 20.0 |
| 10 | 10.0 |
| 20 | 5.0 |
| 25 | 4.0 |
| 50 | 2.0 |
| 100 | 1.0 |
Ora visualizziamo i dati in un diagramma cartesiamo per vedere cosa accade.
Il grafico di una relazione inversamente proporzionale è una curva iperbolica.
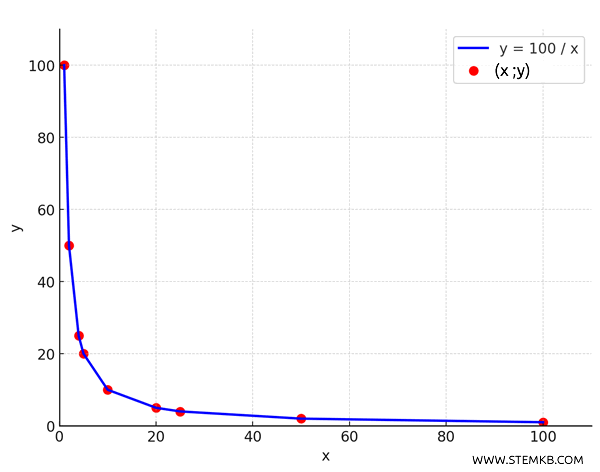
Questo significa che non troverai mai un valore di \(x\) o \(y\) uguale a zero, poiché il prodotto delle due quantità deve essere sempre \(k\), un valore positivo.
La curva si avvicina agli assi senza mai toccarli, dando vita a una forma che sembra "abbracciare" il piano cartesiano.
Quali sono le applicazioni pratiche?
La proporzionalità inversa è un concetto che si applica in numerosi ambiti, dalla matematica pura alle scienze applicate.
Un esempio è la legge di Boyle che descrive la proporzionalità inversa tra pressione (\(P\)) e volume (\(V\)) di un gas, mantenendo la temperatura costante.
$$ P \cdot V = k $$
Dove \(k\) è una costante che dipende dalla quantità di gas e dalla temperatura.
In altre parole, se la pressione aumenta, il volume diminuisce proporzionalmente, e viceversa, purché la temperatura rimanga costante.
La proporzionalità inversa non è solo una questione scientifica o tecnica, è anche una dinamica che osserviamo costantemente nella vita quotidiana. Un esempio comune è il legame tra velocità e tempo necessario per coprire una determinata distanza. Se viaggi a 100 km/h, impiegherai la metà del tempo rispetto a quando viaggi a 50 km/h per raggiungere lo stesso luogo, a parità di altre condizioni (ceteris paribus).
In generale, nella proporzionalità inversa quando una quantità cresce, un’altra diminuisce per bilanciare il sistema in modo armonico.
Questo equilibrio non è solo matematico, ma può essere visto come una metafora della vita stessa: ogni azione ha una reazione, e le relazioni tra le cose spesso seguono schemi logici e armonici.