La proporzionalità quadratica
La proporzionalità quadratica diretta descrive una relazione in cui una grandezza \( y \) è proporzionale al quadrato di un'altra grandezza \( x \). La formula è: $$ y = k \cdot x^2 $$ dove \( k \) è una costante. Questo implica che il rapporto tra \( y \) e \( x^2 \) resta sempre lo stesso: $$ \frac{y}{x^2} = k $$ Questa relazione si rappresenta graficamente come una parabola con vertice nell'origine.
Immaginiamo un esempio semplice: un oggetto che cade liberamente sotto l'azione della gravità.
La formula del moto uniformemente accelerato è un esempio di proporzionalità diretta.
$$ s = \frac{1}{2} g t^2 $$
Dove \( s \) è la distanza percorsa (in metri, m), \( g \) è l'accelerazione di gravità (\( 9,8 \, \text{m/s}^2 \) sulla superficie terrestre) e \( t \) è il tempo di caduta (in secondi, s).
Secondo questa formula, la distanza percorsa dall'oggetto ( \( s \) ), non aumenta in modo lineare con il tempo ( \( t \) ) ma secondo una legge quadratica.
In altre parole, questo significa che la distanza è proporzionale al quadrato del tempo trascorso.
In assenza di attrito o resistenza dell'aria, la distanza percorsa da un oggetto in caduta libera è direttamente proporzionale al quadrato del tempo trascorso.
Un esempio concreto
Immaginiamo un oggetto che cade da una certa altezza.
Vogliamo calcolare la distanza percorsa in funzione del tempo, assumendo \( g = 9,8 \, \text{m/s}^2 \). Utilizziamo la formula sopra per calcolare \( s \) per vari valori di \( t \).
| Tempo (\( t \)) in secondi | Distanza (\( s \)) in metri |
|---|---|
| 1 | \( 4,9 \) |
| 2 | \( 19,6 \) |
| 3 | \( 44,1 \) |
| 4 | \( 78,4 \) |
Ad esempio, dopo $ t = 1 $ secondi l'oggetto è caduto di $ s=\frac{1}{2} \cdot 9,8 \cdot 1^2=4,9 $ metri. Dopo $ t=2 $ secondi è caduto di $ s=\frac{1}{2} \cdot 9,8 \cdot 2^2=19,6 $ metri e via dicendo.
Come si può notare, la distanza percorsa cresce in modo quadratico rispetto al tempo.
Quindi, se calcoliamo il rapporto tra la distanza \( s \) e il quadrato del tempo \( t^2 \), questo rimane costante, confermando la proporzionalità quadratica diretta \( \frac{s}{t^2} \).
| Tempo (\( t \)) | \( s \) in metri | \( t^2 \) in secondi\(^2\) | \( \frac{s}{t^2} \) (\( \text{m/s}^2 \)) |
|---|---|---|---|
| 1 | 4,9 | 1 | 4,9 |
| 2 | 19,6 | 4 | 4,9 |
| 3 | 44,1 | 9 | 4,9 |
| 4 | 78,4 | 16 | 4,9 |
Come possiamo notare, il rapporto \( \frac{s}{t^2} = 4,9 \, \text{m/s}^2 \) e corrisponde alla metà dell'accelerazione di gravità (\( \frac{g}{2} \)), come previsto dalla formula.
Ora tracciamo un grafico con \( t \) sull'asse orizzontale (tempo) e \( s \) sull'asse verticale (distanza).
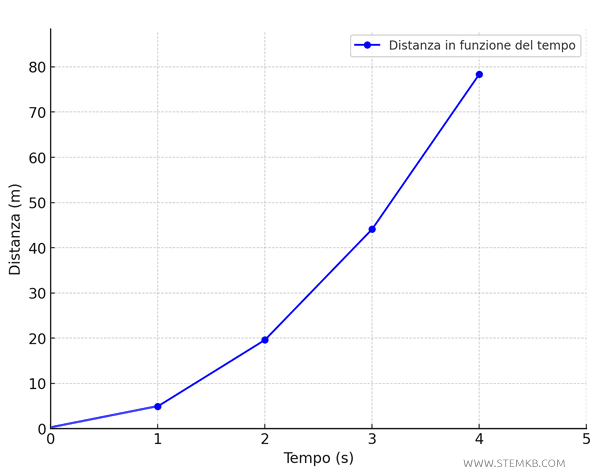
Il grafico di una proporzione quadratica è una parabola con vertice nell'origine. Questo rappresenta visivamente la crescita quadratica della distanza in funzione del tempo.
La proporzionalità quadratica inversa
Esiste anche un'altra forma di proporzionalità quadratica: quella inversa.
Una grandezza \( y \) è inversamente proporzionale al quadrato di \( x \) se il prodotto tra \( y \) e \( x^2 \) è costante. La relazione matematica è: $$ y \cdot x^2 = k \quad \text{o} \quad y = \frac{k}{x^2} $$
Quando si traccia il grafico della formula \( y = k / x^2 \) si ottiene una curva iperbolica che si avvicina agli assi senza mai toccarli.
Un classico esempio di proporzionalità quadratica inversa in fisica riguarda la legge dell'intensità luminosa.
Secondo questa legge, l'intensità luminosa \( I \) è inversamente proporzionale al quadrato della distanza \( d \) dalla sorgente.
$$ I = \frac{k}{d^2} $$
Dove \( I \) è l'intensità della luce (ad esempio, in lumen/m²), \( d \) è la distanza dalla sorgente (in metri), \( k \) è una costante che dipende dalla potenza della sorgente luminosa.
Questo vuole dire che l'intensità della luce si diffonde e si riduce rapidamente con l'aumentare della distanza, secondo una legge quadratica inversa.

Un esempio pratico
Ad esempio, supponiamo di avere una lampadina che emette una luce con un'intensità massima \( k = 100 \) lumen/m² al punto di partenza (\( d = 1 \, \text{m} \)).
Calcoliamo l'intensità luminosa a diverse distanze dalla sorgente.
| Distanza (\( d \)) in metri | Intensità luminosa (\( I \)) in lumen/m\(^2\) |
|---|---|
| 1 | \( 100 \) |
| 2 | \( 25 \) |
| 3 | \( 11,11 \) |
| 4 | \( 6,25 \) |
Ad esempio, a una distanza di un metro ( $ d=1 \ m $ ) l'intensità luminosa è $ \frac{100}{1^2} = 100 $ lumen/mq. A una distanza di due metri ( $ d = 2 \ m $ ) l'intensità luminosa scende a $ \frac{100}{2^2} = 25 $ lumen/mq e via dicendo.
Nota che quando la distanza \( d \) raddoppia (\( d = 2 \)), l'intensità luminosa si riduce a un quarto (\( 25 \, \text{lumen/m}^2 \)). Quando, invece, \( d \) triplica (\( d = 3 \)), l'intensità si riduce a un nono (\( 11,11 \, \text{lumen/m}^2 \)).
Se rappresentassimo questa relazione su un grafico, con \( d \) sull'asse orizzontale e \( I \) sull'asse verticale, otterremmo una curva iperbolica che si avvicina agli assi senza mai toccarli.
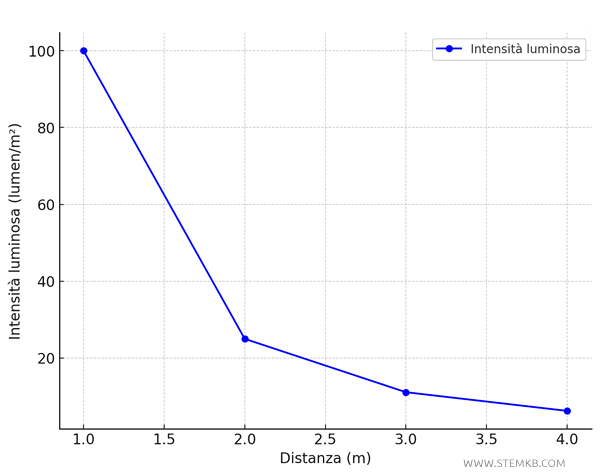
Come puoi vedere, la proporzionalità quadratica inversa descrive molto bene come l'intensità di un fenomeno si riduce rapidamente con l'aumentare della distanza.
In conclusione, queste relazioni matematiche non sono solo formule astratte: descrivono come il mondo fisico si comporta.
Che si tratti di oggetti in caduta libera o dell’intensità della luce, i grafici come parabole e iperboli ci mostrano chiaramente l’ordine nascosto nelle leggi della natura.