Le funzioni
Una funzione $ f $ è una relazione tra due insiemi che associa a ogni elemento del primo insieme (dominio) uno e un solo elemento del secondo insieme (codominio).
Formalmente, una funzione è denotata come \( f: A \rightarrow B \), dove \( f \) è la funzione, \( A \) è il dominio, e \( B \) è il codominio.
- Dominio: L'insieme di tutti i possibili valori di input che la funzione può accettare.
- Codominio: L'insieme di tutti i possibili valori di output che la funzione può produrre.
In notazione, una funzione può essere scritta come \( f(x) \), dove \( x \) rappresenta un elemento del dominio e \( f(x) \) (o \( y \)) è l'elemento del codominio associato.
$$ y = f(x) $$
La variabile \( x \) è la variabile indipendente mentre \( y \) è la variabile indipendente perché dipende dal valore assegnato alla \( x \).
Una volta assegnato un valore a \( x \), il valore di \( y \) è determinato in modo univoco tramie la formula che collega \( x \) a \( y \). Ad esempio, se la funzione \( f(x) \) è data da \( y = 2x \), allora per \( x = 1 \) il valore di \( y \) è \( y = 2 \). Analogamente, per \( x = 2 \) si ottiene \( y = 4 \), e così via.
Esempio
Considera la funzione \( y= f(x) \), dove \( x \) è un numero reale qualsiasi.
$$ f(x) = 3x + 1 $$
Questa funzione associa a ogni numero reale \( x \) un altro numero reale \( y = f(x) \), ottenuto moltiplicando \( x \) per 3 e aggiungendo 1.
Ad esempio, se \( x = 2 \), allora
$$ f(2) = 3(2) + 1 = 7 $$
In questo caso, il valore \( y = 7 \) è l'immagine del valore \( x = 2 \) attraverso la funzione \( y = 2x + 3 \).
Ecco una tabella di valori della funzione \( f(x) = 3x + 1 \) per alcuni valori $ x $ del dominio.
$$
\begin{array}{c|c}
x & y \\
\hline
-2 & -5 \\
-1 & -2 \\
0 & 1 \\
1 & 4 \\
2 & 7 \\
\end{array} $$
In questa tabella, \( y \) rappresenta il valore della funzione \( f(x) = 3x + 1 \) per ogni valore di \( x \).
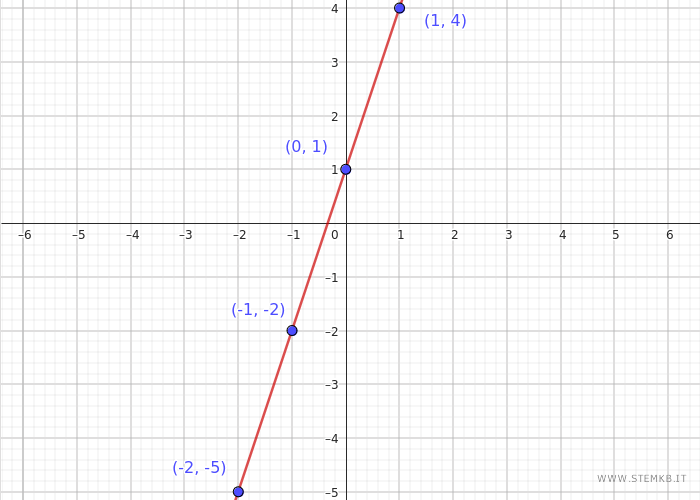
Riportando i dati della tabella sulle coordinate del piano, si può realizzare il grafico della funzione \( f(x) = 3x + 1 \).
Tracciamo questi punti su un piano cartesiano: \((-2, -5)\) , \((-1, -2)\) , \((0, 1)\) , \((1, 4)\) , \((2, 7)\)
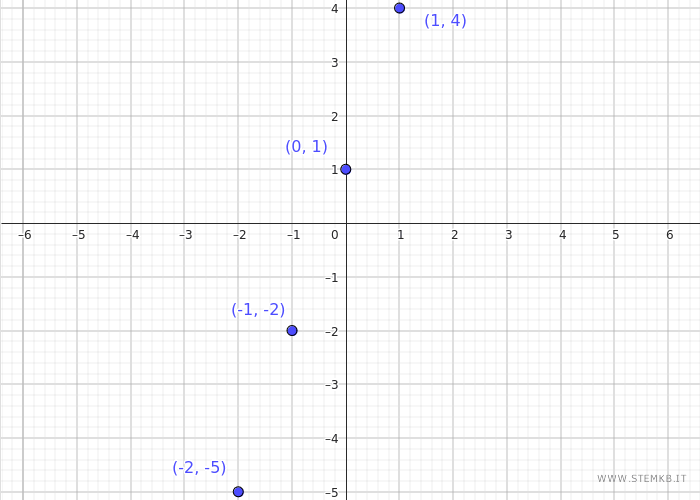
Una volta tracciati questi punti sul piano cartesiano, possiamo unire i punti con una linea retta, dato che la funzione \( f(x) = 3x + 1 \) è una funzione lineare.
Tipi di funzioni
Le funzioni possono essere classificate in vari modi a seconda delle loro proprietà. Ecco una panoramica delle principali categorie:
Funzioni iniettive
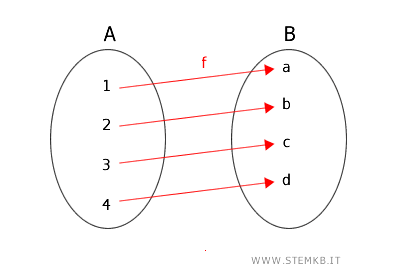
Una funzione \( f: A \rightarrow B \) è iniettiva se elementi distinti di \( A \) vengono mappati su elementi distinti di \( B \).
Questo significa che ogni valore in entrata \( x \) produce un valore in uscita \( y \) univoco e senza ambiguità.
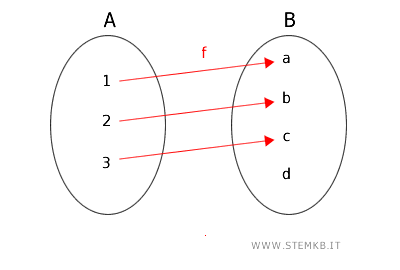
Quindi, se la funzione restituisce lo stesso risultato \( f(x_1) = f(x_2) \) per due valori del dominio $ x_1 $ e $ x_2 $ questo implica che i due valori del dominio sono uguali \( x_1 = x_2 \).
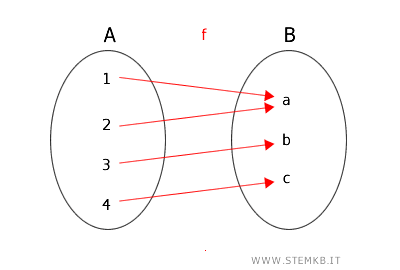
Funzioni suriettive
Una funzione \( f: A \rightarrow B \) è suriettiva se ogni elemento di \( B \) è l'immagine di almeno un elemento di \( A \).
In altre parole, il codominio è completamente coperto dalla funzione, ossia ogni elemento \( y \) del codominio \( B \) è associato ad almeno un elemento \( x \) del dominio \( A \).
Funzioni biiettive
Una funzione è biiettiva se è sia iniettiva che suriettiva. Ciò implica una corrispondenza biunivoca (uno a uno) tra gli elementi del dominio e quelli del codominio.
Ogni elemento di \( A \) è mappato su un elemento unico di \( B \) e viceversa.
Le funzioni iniettive, suriettive e biiettive rappresentano le principali categorie che aiutano a classificare e comprendere meglio il comportamento delle funzioni nelle applicazioni matematiche.