Misura degli angoli
Un angolo è la porzione di piano compresa tra due semirette che hanno un'origine comune \( A \).
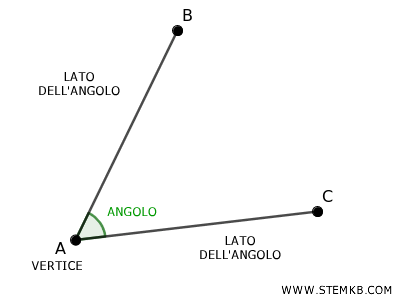
Per misurare un angolo, devi scegliere un’unità di riferimento e assegnargli un valore numerico in base alla sua ampiezza.
Questa unità di misura deve rispettare alcune proprietà fondamentali:
- Due angoli sono congruenti se e solo se hanno la stessa misura.
- Se un angolo ha una misura multipla di un altro angolo, i valori numerici delle loro misure devono riflettere tale proporzione.
- La misura della somma di due angoli è pari alla somma delle misure dei singoli angoli.
Una volta definita l'unità di misura, puoi usarla per misurare l'angolo.
La misura di un angolo è chiamata ampiezza dell’angolo, ed esistono diverse unità di misura per esprimerla. Le principali unità di misure sono i gradi (sistema sessagesimale) e i radianti.
Esempio. Supponia di avere due angoli: uno misura 30° e l’altro 60°. Poiché 60° è il doppio di 30°, puoi dire che il secondo angolo è esattamente il doppio del primo, rispettando la proporzionalità delle misure. Inoltre, se sommi questi due angoli, ottieni un angolo di 90°, che corrisponde a un angolo retto. Questo esempio dimostra come la misura degli angoli tramite i gradi segua tutte le proprietà fondamentali che abbiamo descritto.
Il sistema sessagesimale
Il sistema più comune per misurare gli angoli è quello sessagesimale, introdotto dagli astronomi babilonesi.
In questo sistema, l'unità principale è il grado, indicato con il simbolo °.
Un angolo giro, cioè l'angolo che corrisponde a un’intera rotazione attorno a un punto, è diviso in 360 gradi.
Le principali ampiezze angolari espresse in gradi sono:
- Angolo retto: 90°
- Angolo piatto: 180°
- Angolo giro: 360°
Per una maggiore precisione, il grado è suddiviso in sottomultipli:
- Primo (''): la sessantesima parte di un grado → \(1' = \frac{1}{60}^\circ\).
- Secondo (''): la sessantesima parte di un primo → \(1'' = \frac{1}{60}' = \frac{1}{3600}^\circ\).
Nel calcolo moderno, invece di utilizzare primi e secondi, si preferisce esprimere la misura degli angoli in numeri decimali, per facilitare i calcoli con i dispositivi elettronici.
Esempio
Immagina di guardare un orologio analogico che segna le 3:10:30 e di voler calcolare con precisione l’angolo tra la lancetta delle ore e quella dei minuti, esprimendolo in gradi, primi e secondi.

Quanto si è spostata la lancetta delle ore?
Sai che la lancetta delle ore compie un giro completo di 360° in 12 ore, quindi in 1 ora si sposta di 30°.
$$ 360°:12 = 30° $$
In 1 minuto, la lancetta delle ore si sposta di 0,5°.
Per saperlo ti basta dividere 30° per 60, ossia per il numero di minuti in un'ora.
$$ 30°:60 = 0,5° $$
In 1 secondo, la lancetta delle ore si sposta di 0,0083°.
La logica è la stessa, in questo caso stai dividendo 0,5° per il numero di secondi in un minuto.
$$ 0,5°:60 = 0,0083° $$
Ora calcola lo spostamento dalle 0:00:00 alle 3:10:30:
Ogni ora la lancetta percorre 30°.
$$ 30° \cdot 3 = 90° $$
In 10 minuti, si sposta di:
$$ 10 \cdot 0,5° = 5° $$
In 30 secondi, si sposta di:
$$ 30 \times 0,0083° = 0,249° $$
Quindi la lancetta delle ore è arrivata a 95,249°.
$$ 90° + 5° + 0,249° = 95,249° $$
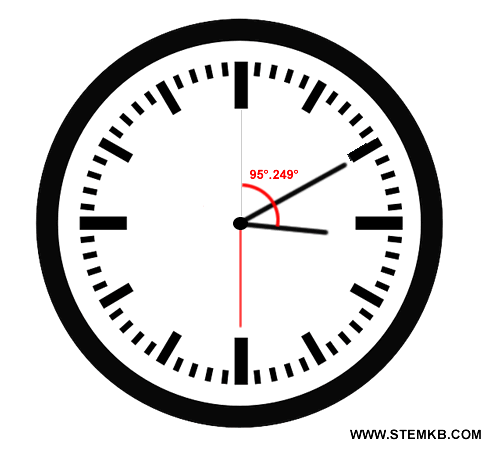
Quanto si è spostata la lancetta dei minuti?
La lancetta dei minuti compie un giro di 360° in 60 minuti, quindi in 1 minuto si sposta di 6°.
$$ 360° : 60 = 6° $$
In 1 secondo, si sposta di 0,1°
$$ 6° : 60 = 0,1° $$
Ora calcola la sua posizione a 10 minuti e 30 secondi.
In 10 minuti, si sposta di:
\[ 10 \times 6° = 60° \]
In 30 secondi, si sposta di:
\[ 30 \times 0,1° = 3° \]
Quindi la lancetta dei minuti è arrivata a 63°.
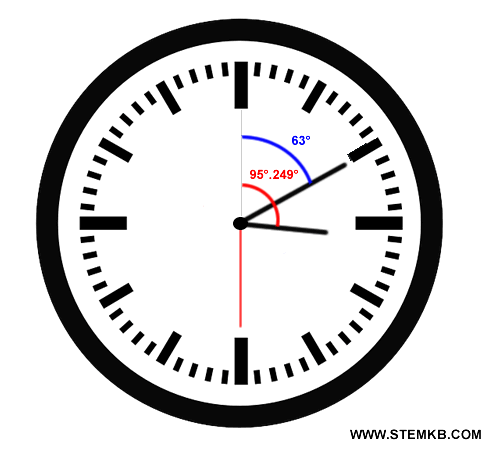
Qual è l'angolo tra le due lancette?
Per saperlo devi calcolare la differenza tra le due misure in valore assoluto.
\[ |95,249° - 63°| = 32,249° \]
Quindi, l'angolo tra la lancetta delle ore e dei minuti è 32,249°.
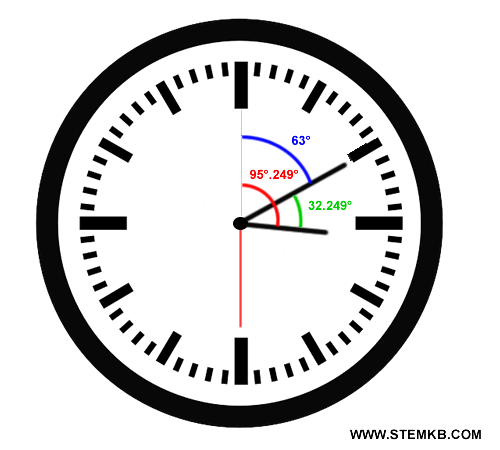
Ora, per ottenere la misura in gradi, primi e secondi, converti la parte decimale:
La parte intera di 32,249° è 32° e resta immutata.
Per convertire la parte decimale 0,249° in primi scrivi:
\[ 0,249 \times 60 = 14,94' \]
Quindi hai 14 primi.
Ora converti la parte decimale in secondi:
\[ 0,94 \times 60 = 56,4'' \]
In conclusione, l’angolo tra le lancette delle ore e dei minuti alle 3:10:30 ha un'ampiezza approssimativa di 32° 14' 56'' (trentadue gradi, quattordici primi e cinquantasei secondi).
Il sistema radiante
Oltre al sistema sessagesimale, esiste un altro metodo di misura degli angoli basato sulla relazione tra un angolo e la lunghezza dell’arco sotteso su una circonferenza di raggio unitario: il radiante.
In questo sistema un angolo giro (360°) corrisponde a \(2\pi\) radianti, perché la lunghezza della circonferenza di raggio 1 è \(2\pi\).
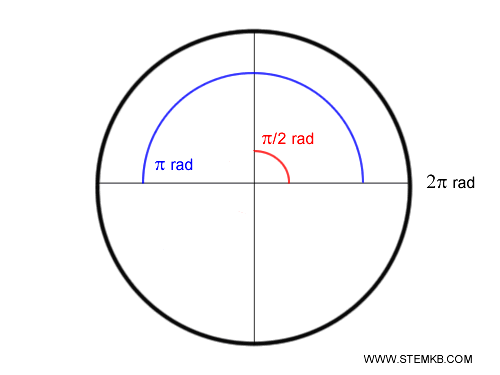
Quindi, un angolo piatto (180°) corrisponde a \(\pi\) radianti e un angolo retto (90°) a \(\frac{\pi}{2}\) radianti.
Il vantaggio del radiante è che semplifica molti calcoli in trigonometria e analisi matematica, rendendo più agevole la manipolazione delle funzioni trigonometriche e delle loro derivate.
Come convertire da gradi a radianti e viceversa
Puoi convertire tra gradi e radianti tramite questa relazione:
$$ 360° = 2 \pi \ \text{rad} $$
Quindi, dividendo entrambi i lati per 360 ottieni la misura di un grado in radianti
$$ \frac{360°}{360} = \frac{2 \pi \ \text{rad}}{360} $$
$$ 1^\circ = \frac{\pi}{180} \ \text{ rad} $$
Con la formula inversa trovi anche la misura di un radiante in gradi
$$ \text{ rad} = \frac{180}{\pi}^\circ $$
Questo significa che \(180^\circ = \pi\) radianti, \(90^\circ = \frac{\pi}{2}\) radianti, \(45^\circ = \frac{\pi}{4}\) radianti, ecc.
Questa relazione ti permette di convertire agevolmente tra gradi e radianti in qualsiasi problema.
Ad esempio, nell'orologio l'angolo tra le lancette dei minuti e delle ore è 32,249° gradi. Per convertirlo in radianti basta applicare la prima formula. $$ 32,249° \cdot \frac{\pi}{180°} \approx 0,56 \ rad $$
Quale sistema scegliere? Sessagesimale o radianti?
In conclusione, il sistema sessagesimale, con i suoi 360 gradi, è quello più diffuso nella vita quotidiana e in applicazioni pratiche come la navigazione e la cartografia.
Il sistema radiante, invece, è preferito in ambiti più teorici, come la fisica e l'analisi matematica, per la sua semplicità nei calcoli con le funzioni trigonometriche.