Uniformly Accelerated Rectilinear Motion
Uniformly accelerated rectilinear motion describes the movement of an object along a straight path with a constant acceleration.
The object's velocity increases linearly over time, starting from an initial velocity.
The object's position changes according to a quadratic function of time.
Let's break down the concept of uniformly accelerated rectilinear motion with simple explanations and practical examples.
Position Formula
The formula for position in uniformly accelerated motion is:
\[ s = s_0 + v_0 t + \frac{1}{2} a t^2 \]
This formula states that the position at any given time (s) is equal to the initial position (\(s_0\)) plus the product of the initial velocity (\(v_0\)) and the elapsed time (t), plus half the product of the acceleration (a) and the square of the time (t²).
Where:
- \( v \) is the velocity at any given moment.
- \( v_0 \) is the initial velocity (velocity at the start, when t = 0).
- \( t \) is the elapsed time.
- \( a \) is the constant acceleration (the rate of change of velocity over time).
- \( s_0 \) is the initial position (position at the start, when t = 0).
- \( s \) is the position at any given moment.
If the initial position and initial velocity are both zero (\(s_0 = 0\) and \(v_0 = 0\)), the position formula simplifies to: $$ s = \frac{1}{2} a t^2 $$
Velocity Formula
The formula for velocity in uniformly accelerated motion is:
\[ v = v_0 + at \]
This formula indicates that the velocity at any given time (v) is equal to the initial velocity (\(v_0\)) plus the product of the acceleration (a) and the elapsed time (t).
If the initial position and initial velocity are zero (\(s_0 = 0\) and \(v_0 = 0\)), the velocity formula becomes: $$ v = at $$
Practical Example
Imagine you are holding a ball at a certain height.
Initially, the ball's velocity is zero because it is not moving.
$$ v_0 = 0 $$
When you let go of the ball, it accelerates due to gravity (g ≈ 9.8 m/s²), which pulls everything towards the center of the Earth.
After one second (t = 1), the ball's falling velocity will be:
\[ v = 9.8 \, \text{m/s}^2 \cdot 1 \, \text{s} = 9.8 \, \text{m/s} \]
After two seconds (t = 2), the ball's falling velocity will be:
\[ v = 9.8 \, \text{m/s}^2 \cdot 2 \, \text{s} = 19.6 \, \text{m/s} \]
After three seconds (t = 3), the ball's falling velocity will be:
\[ v = 9.8 \, \text{m/s}^2 \cdot 3 \, \text{s} = 29.4 \, \text{m/s} \]
The ball's position after three seconds will be:
\[ s = \frac{1}{2} \cdot 9.8 \, \text{m/s}^2 \cdot (3 \, \text{s})^2 = \frac{1}{2} \cdot 9.8 \cdot 9 = 44.1 \, \text{m} \]
So, after just three seconds, the ball will have reached a velocity of 29.4 m/s and fallen 44.1 meters.
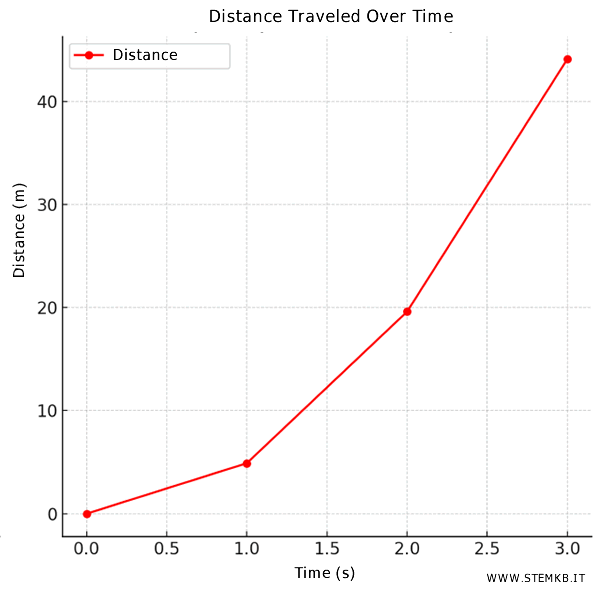
Here is a table showing the velocity and distance covered by the ball at different times, with the acceleration due to gravity \( g \approx 9.8 \, \text{m/s}^2 \):
\[
\begin{array}{|c|c|c|}
\hline
\text{Time } (t) \text{ [s]} & \text{Velocity } (v) \text{ [m/s]} & \text{Distance } (s) \text{ [m]} \\
\hline
0 & 0 & 0 \\
\hline
1 & 9.8 & 4.9 \\
\hline
2 & 19.6 & 19.6 \\
\hline
3 & 29.4 & 44.1 \\
\hline
\end{array}
\]
From this data, we can plot the distance-time graph.
As you can see, the ball's falling velocity increases over time.
Note that in the absence of air resistance, all objects fall with the same acceleration regardless of their mass.
This acceleration is due to gravity and has an approximate value of \( g \approx 9.8 \, \text{m/s}^2 \).
According to Galileo Galilei's law of falling bodies, in a vacuum (where there is no air resistance), all objects fall with the same gravitational acceleration.
This means that a feather and a cannonball, dropped at the same time from the same height, will hit the ground simultaneously.
A famous experiment demonstrating this principle was conducted by astronaut David Scott on the Moon during the Apollo 15 mission. He dropped a hammer and a feather simultaneously. Since the Moon has no atmosphere and therefore no air resistance, both objects fell with the same acceleration and hit the lunar surface at the same time. This experiment proved that in the absence of air resistance, an object's mass does not affect its falling speed.