Uniform Rectilinear Motion

Uniform rectilinear motion occurs when an object moves in a straight line at a constant speed. There are no forces acting to change the object's speed.

The main characteristics of this motion are:

The motion takes place in a straight line.
The speed $ v $ remains constant.

Law of Uniform Rectilinear Motion

The formula to describe uniform rectilinear motion is:

$$ s = s_0 + vt $$

Where:
- $ t $ is the elapsed time.
- $ s $ is the object's position at any time $ t $.
- $ s_0 $ is the initial position of the object at time $ t = 0 $.
- $ v $ is the constant speed.

Space-Time Graph

Imagine a graph where the vertical axis represents the position $ s $ and the horizontal axis represents the time $ t $.

For uniform rectilinear motion, the graph is a straight line.

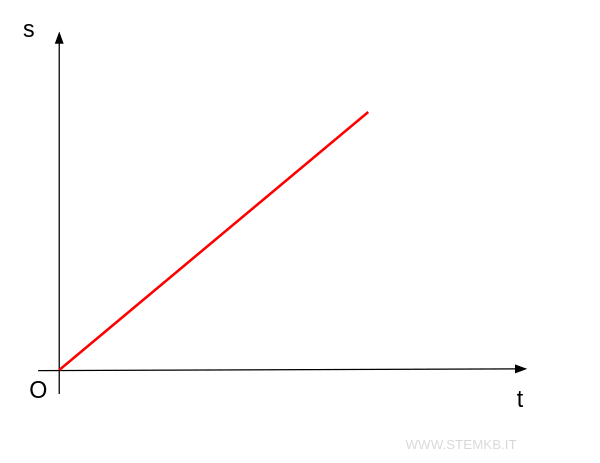
space-time graph of uniform rectilinear motion

The straight line intersects the position axis at point $ s_0 $ when time $ t $ is 0, marking the initial moment of motion.

In other words, if you start from an initial position $ s_0 $, the final position $ s $ after a certain time $ t $ will be $ s_0 + vt $.

If the initial position is $ s_0 = 0 $ (i.e., you start from the origin), the formula simplifies to: $$ s = vt $$

A Practical Example

Let's go through a practical example to illustrate the concept of uniform rectilinear motion.

Imagine a car moving along a straight road at a constant speed of 60 km/h.

The car moves at a constant speed $ v = 60 $ km/h for a time $ t = 2 $ hours.

Assume we start measuring the car's position from a specific starting point, denoted as $ s_0 = 0 $ km.

We use the formula for uniform rectilinear motion:

$$ s = s_0 + vt $$

The given values are:

$ s_0 = 0 $ km (initial position)
$ v = 60 $ km/h (constant speed)
$ t = 2 $ hours (elapsed time)

Now, let's substitute these values into the formula:

$$ s = 0 + 60 \times 2 $$

$$ s = 0 + 120 $$

$$ s = 120 $$

After 2 hours, the car will be 120 km from the starting point.

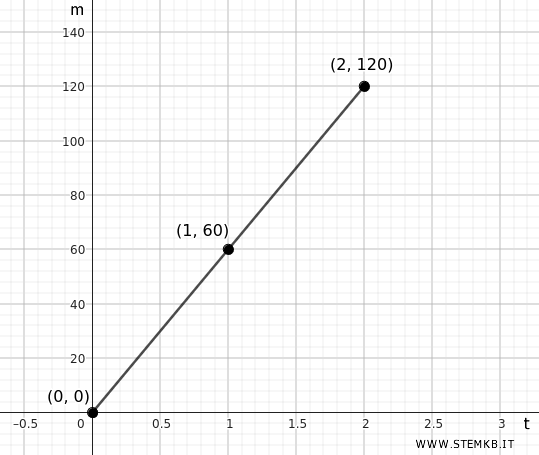
Now let's represent this motion on a space-time graph:

The horizontal axis (x) represents time $ t $ in hours, while the vertical axis (y) represents position $ s $ in kilometers.

For each hour that passes, the car travels 60 km. Therefore, the graph will be a straight line starting from the origin (0,0) and rising steadily to the right, with a slope representing the constant speed of 60 km/h.

Here’s a table showing the car’s position at different times:

\[
\begin{array}{|c|c|}
\hline
\text{Time (hours)} & \text{Position (km)} \\
\hline
0 & 0 \\
1 & 60 \\
2 & 120 \\
\hline
\end{array}
\]

This table shows how the car’s position changes linearly with time, following the law of uniform rectilinear motion $ s = s_0 + vt $.

Thus, the point (1,60) on the graph represents the car’s position after 1 hour, while the point $ (2, 120) $ represents the car’s position after 2 hours.

motion graph

I hope this example helps you better understand the concept of uniform rectilinear