La topologia

La topologia è una disciplina matematica che esplora le proprietà degli spazi che rimangono costanti attraverso trasformazioni continue, come stiramenti e deformazioni, escludendo però gli strappi o le incollature.

Questo campo di studio si focalizza su concetti fondamentali quali la continuità e il confine, indagando le caratteristiche essenziali degli oggetti geometrici che resistono a cambiamenti drastici.

Uno degli esempi più illustrativi della topologia è la dimostrazione che una ciambella e una tazza da caffè sono considerate equivalenti in termini topologici perché entrambi contengono un unico "buco". In pratica, immagina di poter modellare una ciambella di argilla senza strapparla né incollarla. Con un po' di manipolazione, puoi trasformarla in una tazza, estendendo una parte dell'argilla per formare il manico, dimostrando così che hanno la stessa "topologia". Questo tipo di equivalenza, chiamata omeomorfismo, implica che le trasformazioni coinvolte sono continue e reversibili.

La topologia si divide in diverse sotto-aree, ognuna con il proprio focus e metodologia.

• Topologia generale
  La topologia generale si dedica allo studio di concetti basilari come spazi, continuità e compatezza, senza fare affidamento su metodi derivati dal calcolo.
• Topologia algebrica
  La topologia algebrica utilizza strumenti algebrici per analizzare gli spazi topologici.
• Topologia differenziale
  La topologia differenziale si concentra su proprietà e strutture che necessitano di calcolo.

Studiare la topologia permette di avere una comprensione profonda di molte questioni matematiche e fisiche, facendo luce sulla struttura intrinseca degli spazi, sia che si tratti di configurazioni puramente astratte sia che si tratti di forme nello spazio fisico.

Inoltre, le idee topologiche trovano applicazioni in diversi campi che si estendono ben oltre la pura matematica, dalla fisica quantistica all'informatica teorica, rendendo la topologia un campo di studio estremamente ricco e interdisciplinare.

La capacità di trascendere le forme specifiche e vedere oltre l'apparenza superficiale per concentrarsi sulle proprietà fondamentali, profonde e invariate degli spazi, permette alla topologia di rivelare connessioni inaspettate tra oggetti che a prima vista sembrano completamente diversi, come la ciambella e la tazza di caffè nell'esempio classico dell'equivalenza topologica. 

In conclusione, la topologia ci insegna che le verità più profonde e più universali a volte richiedono di guardare il mondo in modi che sfidano le nostre intuizioni e percezioni immediate.

Quindi, la topologia non è solo uno studio sui limiti della deformazione e della continuità, è anche una fonte di ispirazione per vedere il mondo in modi nuovi e più profondi, sottolineando quanto sia importante rimanere aperti a nuove prospettive e nuovi modi di pensare.

La topologia degli insiemi

La topologia degli insiemi, nota anche come topologia generale o topologia puntuale, è una branca fondamentale della topologia matematica.

Quest'area si concentra sullo studio delle strutture topologiche più generali e delle loro proprietà.

Include l'esame di concetti come apertura e chiusura di insiemi, continuità, convergenza di sequenze, compattezza, connessione e molte altre proprietà che riguardano la struttura degli spazi topologici.

La topologia degli insiemi serve come base per molte altre parti della topologia, come la topologia algebrica e la topologia differenziale, fornendo un quadro concettuale e tecnico per trattare questioni di continuità e limite in contesti molto generali.

Questo campo è essenziale per comprendere come le proprietà topologiche influenzano il comportamento di funzioni e spazi in una vasta gamma di contesti matematici e applicativi.

Esempio

Un esempio interessante che illustra il potere della topologia di rivelare connessioni inaspettate tra concetti apparentemente diversi si trova nel "Teorema dei quattro colori".

Questo teorema, che afferma che quattro colori sono sufficienti per colorare qualsiasi mappa piana in modo che regioni adiacenti abbiano colori diversi, ha implicazioni profonde e applicazioni dirette nella teoria dei grafi, un campo strettamente legato alla topologia.

Per fare un esempio pratico proviamo a colorare gli stati europei facendo in modo che ogni stato abbia un colore diverso rispetto ai paesi confinanti.

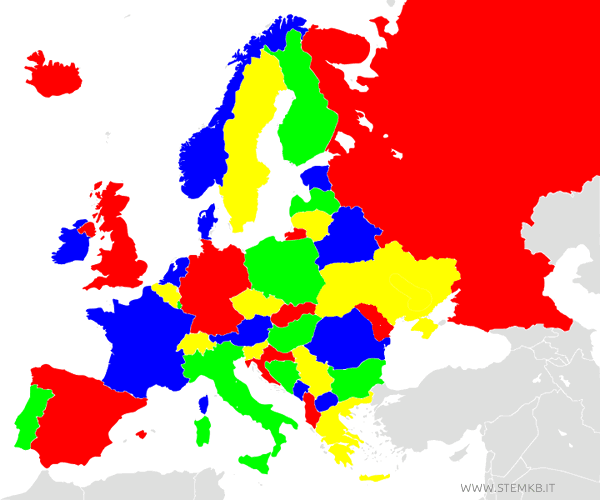
Nella topologia, una mappa può essere vista come un grafo planare, dove le regioni della mappa sono vertici del grafo e i confini tra regioni sono gli archi che li collegano.

Ad esempio, la mappa degli stati europei possiamo rappresentarla con un grafo, conservando tutte le informazioni più importanti sui confini.

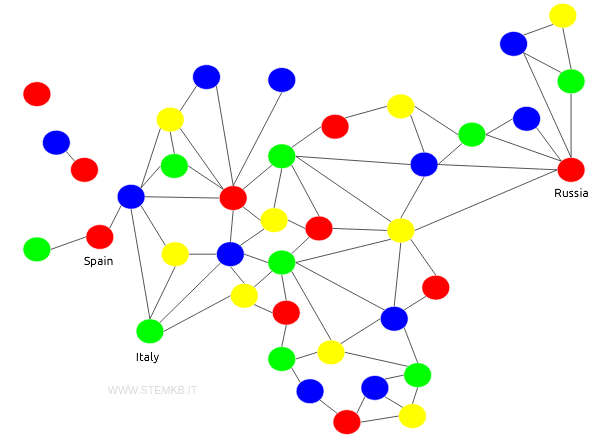
La posizione dei nodi del grafo non è importante, ciò che conta è la connessione tra gli archi.

Quindi, il grafo potrebbe presentarsi anche in una forma diversa mantenendo però se stesse informazioni.

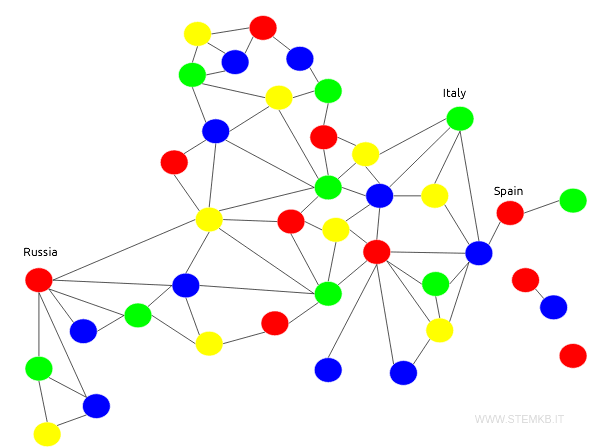
Il problema del colorare una mappa diventa quindi un problema di colorare i vertici di un grafo in modo che non ci siano due vertici adiacenti dello stesso colore.

Questo problema, pur essendo formulato in termini geometrici e topologici, ha significative applicazioni pratiche, come nella scelta di frequenze per le stazioni radio in aree geografiche adiacenti per evitare interferenze, o nella creazione di orari in modo che le lezioni che condividono alcuni studenti o risorse non si sovrappongano.

L'approccio topologico al problema dei quattro colori dimostra come un'idea matematica possa essere trasformata in uno strumento pratico per risolvere problemi concreti in diversi ambiti, evidenziando la natura interconnessa della conoscenza e l'importanza di pensare oltre i confini tradizionali delle discipline.