Principio di identità dei polinomi
Due polinomi P1 e P2 in forma normale sono identici se e solo se hanno lo stesso grado e gli stessi coefficienti delle lettere che compaiono nelle espressioni. $$ \forall \ x \ \ \Rightarrow P_1(x) = P_2(x) $$
Ad esempio, considera i seguenti polinomi
$$ P_1(x) = 1-x^2 $$
$$ P_2(x) = -(x^2-1) $$
Sono due polinomi dello stesso grado, quindi la prima condizione è verificata.
Per capire se anche la seconda condizione è soddisfatta, prova a trasformarli in modo tale che i coefficienti delle variabili coincidano.
In questo caso la soluzione è molto semplice, puoi trasformare il secondo polinomio in questa forma equivalente
$$ P_1(x) = 1-x^2 $$
$$ P_2(x) = -(x^2-1) = -x^2 +1 = 1-x^2 $$
Quindi, i due polinomi hanno lo stesso grado (2) e gli stessi coefficienti dei termini x2, x1 e x0 ossia 1, 0, -1
$$ P_1 = P_2 $$
Pertanto, sono due polinomi identici.
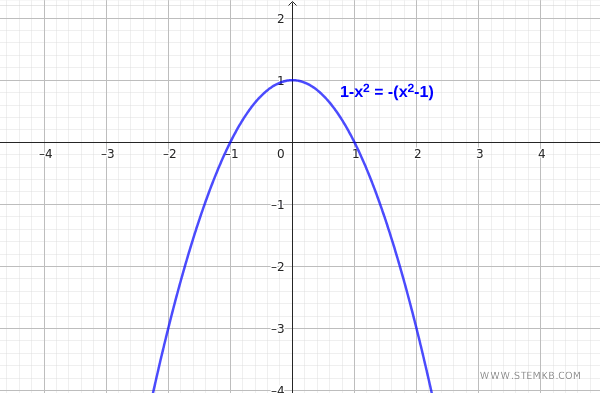
Nota. Quando due polinomi sono identici assumono lo stesso valore quando gli attribuisci gli stessi valori alle lettere. Quindi, hanno la stessa forma del grafico. Vale anche l'inverso. Se due polinomi hanno la stessa forma, allora sono polinomi identici.