Support Vector Machine
L'algoritmo Support Vector Machine è usato nel machine learning supervisionato per risolvere problemi di classificazione e di regressione. Sono dette macchine a vettori di supporto.
Il processo di addestramento riceve in input un dataset di training composto da molti esempi. Ogni riga del dataset è un esempio identificato da un vettore xi con n caratteristiche (features) e un'etichetta (label).
$$ ( X , y ) $$
Dove X è una matrice composta dai vettori xi. Ogni vettore xi è l'insieme delle caratteristiche di un esempio e individua un punto nello spazio a n dimensioni. Il vettore y contiene le etichette (label) ossia le risposte corrette di ogni esempio.
L'algoritmo individua un iperpiano in grado di dividere il set di dati in due classi.
Il confine che separa le classi è detto confine decisionale (decisione boundary).
Esempio. Se gli esempi sono composti da due caratteristiche (features), l'iperpiano è una semplice linea che separata l'insieme dei dati in due categorie.
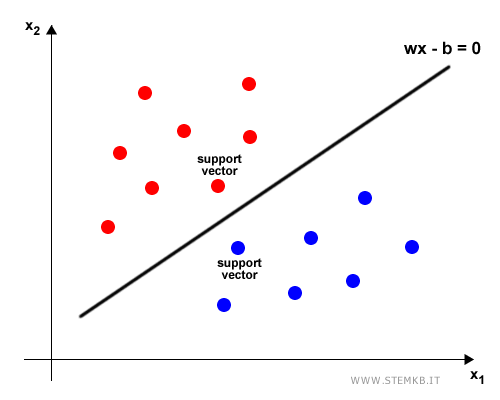
Se le caratteristiche sono tre l'iperpiano è un piano nello spazio a tre dimensioni. Se le caratteristiche sono più di tre, l'iperpiano è un piano nello spazio multidimensionale.
I punti più vicini all'iperpiano sono maggiormente soggetti all'aggiunta dei nuovi dati. Una piccola variazione dell'iperpiano può modificare la loro classificazione. Per questa ragione sono detti support vector.
I punti più lontani dall'iperpiano, invece, hanno maggiore probabilità d'essere classificati correttamente dall'algoritmo.
La distanza tra i support vector e il confine decisionale è detto margin (margine).

Nota. Il margine misura la distanza tra i due piani wx-b=1 e wx-b=-1. La distanza tra i due piani è 2/||w||. Quindi, più piccola è la norma euclidea ||w||, più ampio è il margine. Per questa ragione l'algoritmo minimizza la norma.
Un ampio margine garantisce una buona generalizzazione dell'algoritmo nel classificare i nuovi dati.
Pertanto, la classificazione degli algoritmi SVM è affidabile se la distanza tra l'iperpiano e i support vector è elevata.
L'iperpiano è individuato dall'equazione
$$ wx - b = 0 $$
Nota. Il vettore w={w1, w2, ... , wj} è composto da j numeri reali detti pesi, uno per ogni caratteristica x={x1, x2, ... , xj} del set di dati. Quindi wx è una combinazione lineare del tipo w1x1+w2x2+...+wjxj.
L'algoritmo SVM trova i valori ottimali di w e b risolvendo un problema di ottimizzazione durante il processo di training (addestramento).
Una volta trovati, li usa nella funzione segno (sign) per classificare i dati.
$$ y = sign(w*x-b*) $$
Il valore y assume questi valori
- +1 se la funzione w*x-b*≥0
- -1 se la funzione w*x-b*≤0
Questa funzione è detta modello statistico o soltanto modello.
Nota. In questo semplice modello il limite decisionale è lineare. Si presenta come una retta o un piano che separa i dati. In altri modelli il limite decisionale è non lineare e si presenta come una curva.