Regressione logistica
La regressione logistica è un modello statistico (modello logit) usato negli algoritmi di classificazione del machine learning per ottenere la probabilità di appartenenza a una determinata classe.
L'algoritmo di classificazione basato sulla regressione logistica è del tipo ML supervisionato.
Si basa sull'utilizzo della funzione logistica (sigmoid) che converte i valori reali in un valore compreso tra 0 e 1.
Nota. Nonostante il nome dell'algoritmo "regressione logistica" (logistic regression) faccia pensare a un algoritmo di regressione, perché la funzione logistica è simile alla regressione lineare, si tratta di un algoritmo di classificazione.
Nella fase di addestramento l'algoritmo riceve in input un dataset di training composto da N esempi. Ogni esempio è composto da m attributi X e da un'etichetta y che indica la corretta classificazione.
Esempio di training dataset
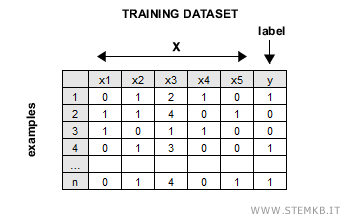
L'algoritmo individua una vettore dei pesi W da associare al vettore degli attributi Xm degli esempi, in modo tale da massimizzare la percentuale di risposte corrette (o minimizzare quelle sbagliate).
La combinazione lineare z dei pesi L per gli attributi X fornisce una risposta del sistema per ogni esempio del training dataset.
$$ z = W \cdot X = w_1 x_1 + ... + w_m x_m $$
Nella regressione logistica la combinazione lineare z è l'argomento della funzione logistica che lo traduce in un valore compreso tra 0 e 1. $$ f(z) = [0,1] $$
Il risultato della funzione logistica è usato come funzione di attivazione dei nodi della rete neurale.
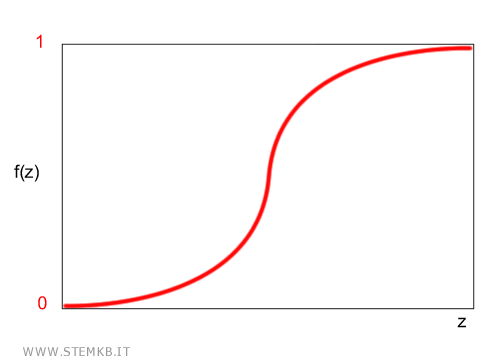
Ad esempio, se viene fissato come parametro di soglia il valore 0.6, quando f(z)>0.6 il nodo viene attivato. Viceversa è disattivo.
$$ \begin{cases} 1 \:\: if \:\: f(z)>0.6 \\ \\ 0 \:\: else \end{cases} $$
Per scegliere la distribuzione W* migliore l'algoritmo utilizza un'altra funzione di massimizzazione della probabilità L.
$$ max \: L(W) = \sum_{i=1}^N y_i \log f(z_{(i)}) (x) + (1-y_i) \log (1-f(z_{(i)})) $$
La sommatoria confronta tutte le risposte del modello con le risposte corrette calcolando la log-probabilità.
Al termine dell'addestramento l'algoritmo produce un modello, utilizzabile per classificare qualsiasi altro esempio non compreso nel training set.