I modelli di Markov nascosti (HMM)

Un modello nascosto di Markov (HMM, Hidden Markov Model) è un modello statistico che usa un processo di Markov non osservabile (nascosto) per generare una sequenza di osservazioni indirette. E' caratterizzato da:

• Processo latente o nascosto (X)
  E' un processo che non possiamo osservare direttamente. Questo processo segue le regole di un modello di Markov, il che significa che lo stato attuale dipende solo dallo stato immediatamente precedente.
• Processo osservabile (Y)
  Esiste anche un processo osservabile (Y) i cui risultati sono influenzati dal processo latente (X). Osserviamo solo gli esiti di Y, che sono indirettamente influenzati dagli stati nascosti di X.
• Dipendenza e indipendenza condizionale
  Un aspetto cruciale degli HMM è che l'esito osservabile al tempo t, ossia Y(t), è influenzato solo dallo stato latente al tempo t, ossia X(t). Gli stati o osservazioni passati (prima di t) non influenzano direttamente l'osservazione corrente, a condizione che lo stato latente corrente sia noto.

  Quindi, per comprendere e utilizzare gli HMM, è necessario stimare dei parametri che includono le probabilità di transizione tra gli stati latenti e le probabilità di emissione (che collegano gli stati latenti alle osservazioni).

Pertanto, i modelli di Markov nascosti (Hidden Markov Model) hanno degli stati interni che non possiamo vedere direttamente. Sono le informazioni che il modello dovrà scoprire, prevedere o classificare.

Questi stati sono detti stati nascosti (hidden) e rappresentano le condizioni sottostanti di un sistema.

Ad esempio, gli strati nascosti potrebbero rappresentare il tempo atmosferico in una data giornata, che può essere "soleggiato" o "piovoso", ma non è direttamente osservabile.

Le osservazioni, invece, sono tutti i dati che possiamo effettivamente vedere o misurare.

Ovviamente, sono i dati che hanno un certo collegamento con ciò che vogliamo scoprire.

Nell'esempio del tempo, un'osservazione utile potrebbe essere l'attività di una persona che osserviamo mentre cammina in strada, come "camminare velocemente", "fare shopping", "usare l'ombrello", "pulire", "fermarsi a parlare con altri", ecc.

Le probabilità di transizione descrivono come gli stati nascosti cambiano nel tempo.

Per esempio, potrebbe esserci una certa probabilità che un giorno soleggiato segua un altro giorno soleggiato, o che cambi in un giorno piovoso.

Infine, le probabilità di emissione collegano gli stati nascosti alle osservazioni.

Ci dicono quanto è probabile osservare una certa azione (come "camminare velocemente") quando il tempo è in uno stato specifico (come "soleggiato" oppure "piovoso").

L'idea di base di un HMM è di usare le osservazioni per fare inferenze sugli stati nascosti.

Ad esempio, se sappiamo che una persona tende a "camminare lentamente" quando fa bel tempo, e vediamo che sta "camminando piano", possiamo inferire che probabilmente il tempo è soleggiato.

Esempio

Un esempio di modello di Markov nascosto in forma discreta è il "problema dell'urna".

Immagina una stanza con diverse urne (x1, x2, x3), ciascuna contenente una proporzione nota di palline etichettate (y1, y2, y3).

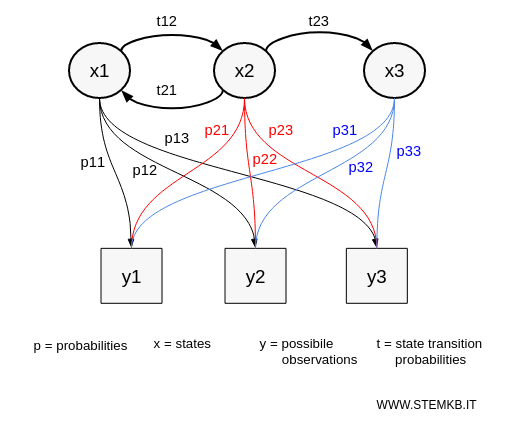
Un genio sceglie un'urna e estrae una pallina, che poi viene messa su un nastro trasportatore dove un osservatore può vedere solo la sequenza di palline, ma non le urne da cui vengono estratte.

La scelta dell'urna da parte del genio dipende solo dall'urna scelta immediatamente prima, quindi si tratta di un processo di Markov. Nella scelta dell'urna ci sono delle probabilità di transizione (t12, t21, t23).

L'osservatore può vedere solo la sequenza di palline estratte ma non il processo di scelta delle urne, quindi questo processo è "nascosto" (hidden).

Anche conoscendo la composizione delle urne, l'osservatore non può essere sicuro da quale urna proviene una specifica pallina osservata (y1, y2, y3), ma può calcolare la probabilità che provenga da ciascuna delle urne x1, x2, x3.