Gli alberi decisionali

Un algoritmo decisionale (decision tree) è un modello predittivo del machine learning supervisionato. E' usato sia per risolvere problemi di classificazione che problemi di regressione.

L'addestramento utilizza una serie di domande sulle caratteristiche (feature) per formulare una previsione in uscita (target) che può essere discreta o continua.

L'algoritmo decision tree suddivide i dati in sottoinsiemi composti da attributi diversi, fin quando trova dei sottoinsiemi che raggiungono un medesimo obiettivo con minore incertezza possibile.

L'incertezza di un sottoinsieme può essere misurata con diversi metodi, tra i quali l'entropia (H) o quantità attesa delle informazioni (I(.

$$ I(X) = - \sum_{i=1}^n P(x_i) \log_s p(x_i) $$

Dove s è il numero degli eventi possibili o delle risposte possibili a una domanda.

Esempio. Nel caso del lancio di una moneta c'è la probabilità p₁=0.5 che si verifichi testa e la probabilità p₂=0.5 che si verifichi croce. La quantità attesa di informazione (o entropia) è $$ I = - ( \frac{1}{2} \log_2 \frac{1}{2} + \frac{1}{2} \log_2 \frac{1}{2} ) = 1 $$ L'entropia è al massimo perché l'incertezza è molto elevata. Viceversa, se una monetà è truccata per far uscire sempre testa, p₁=1 e P₂=0. In questo caso la quantità attesa di informazione (o entropia) è $$ I = - ( 1 \log_2 1 + 0 \log_2 0 ) = 0 $$ L'entropia è nulla perché il risultato è certo.

Il guadagno dell'informazione misura la differenza di entropia dopo la suddivisione di un sottoinsieme in base a un attributo.

Dal punto di vista grafico l'output è un grafo aciclico (albero) in cui ogni nodo è un attributo. I rami di ogni nodo sono i possibili valori dell'attributo.

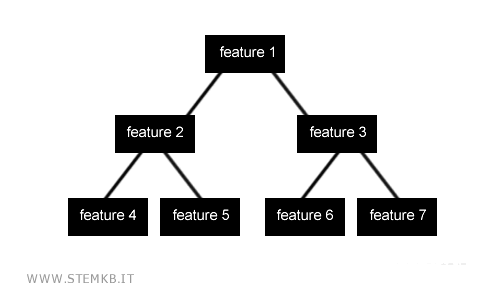
L'obiettivo dell'algoritmo è individuare la sequenza di attributi che riduce l'incertezza.

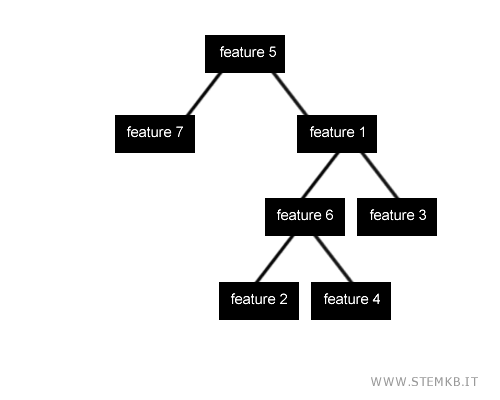
Il guadagno (gain) è la differenza tra l'entropia prima e dopo la suddivisione.

L'albero con il guadagno maggiore è quello ottimale rispetto al dataset di training utlizzato.