L'ortocentro su Geogebra

In questo tutorial ti spiego come trovare l'ortocentro di un triangolo usando Geogebra.

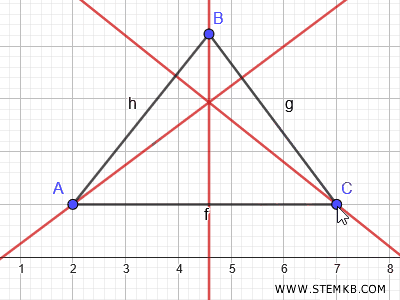
Cos'è l'ortocentro? In un triangolo l'ortocentro è il punto in cui si intersecano le tre altezze del triangolo. E' un punto interno al triangolo se è acutangolo oppure esterno se è ottusangolo.

Per prima cosa, seleziona lo strumento Punto.

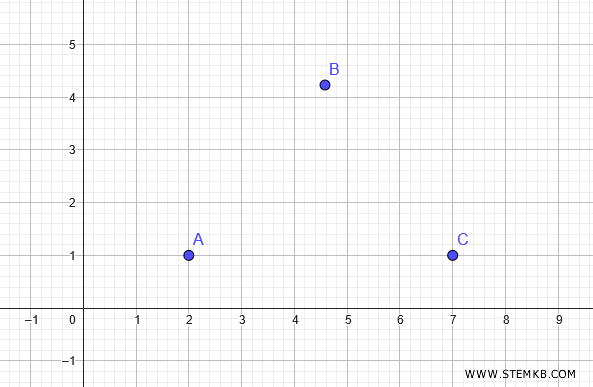
Poi aggiungi tre punti A, B, C sul piano di Geogebra.

Ora seleziona lo strumento Segmento.

Traccia tre segmenti AB, AC, BC.

In questo modo hai ottenuto un triangolo.

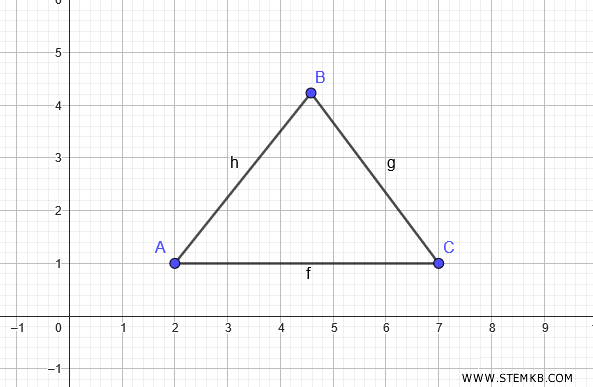
A questo punto seleziona lo strumento Retta perpendicolare.

Clicca su un punto qualsiasi del segmento BC, esclusi gli estremi, poi clicca sul punto A.

Geogebra disegna l'altezza dal vertice A.

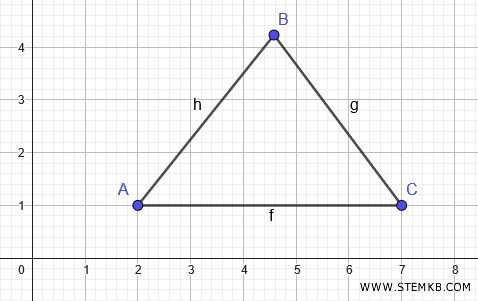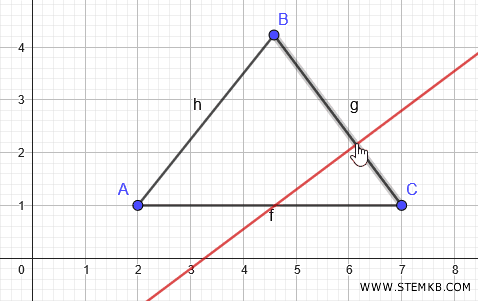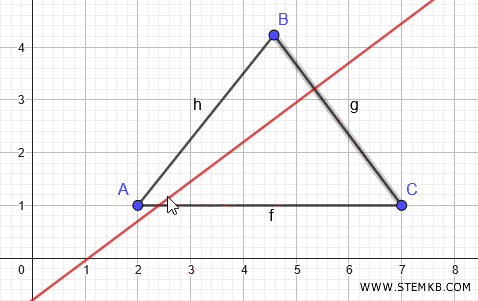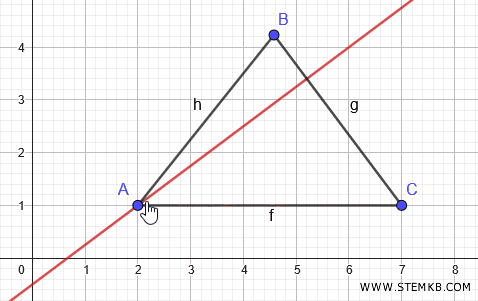
L'altezza è un segmento perpendicolare al lato opposto al vertice A, ossia BC, in quanto forma un angolo di 90°

Ripeti lo stesso procedimento per gli altri due punti.

Seleziona lo strumento Retta perpendicolare.

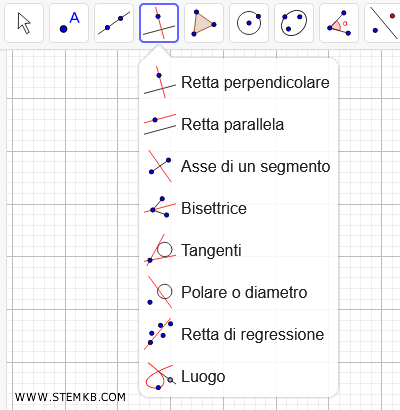
Clicca su un punto qualsiasi del segmento AC, esclusi gli estremi, poi clicca sul punto B.

Geogebra disegna l'altezza del triangolo misurata dal vertice B.

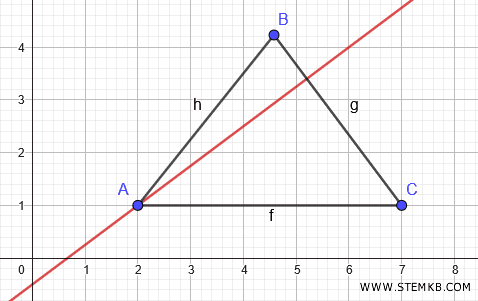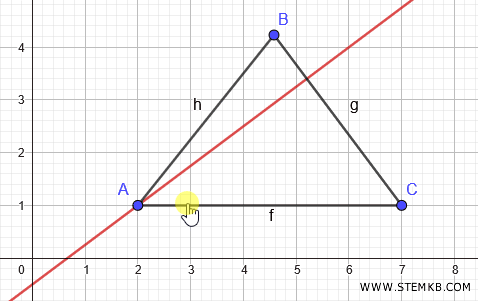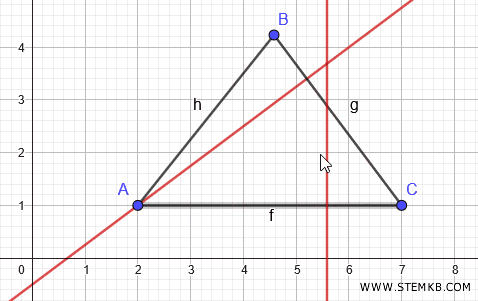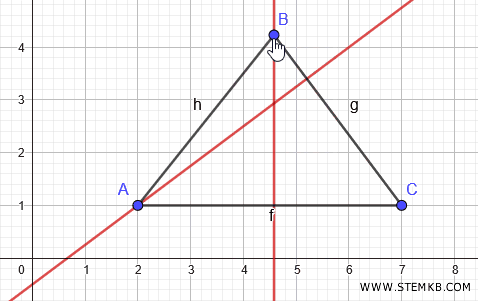
Infine, seleziona di nuovo lo strumento Retta perpendicolare.

Clicca su un punto qualsiasi del segmento AB, esclusi gli estremi, poi clicca sul punto C.

Geogebra disegna l'altezza del triangolo dal vertice C.

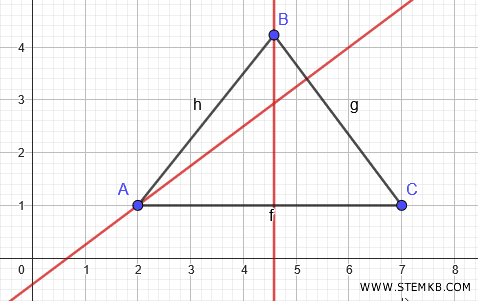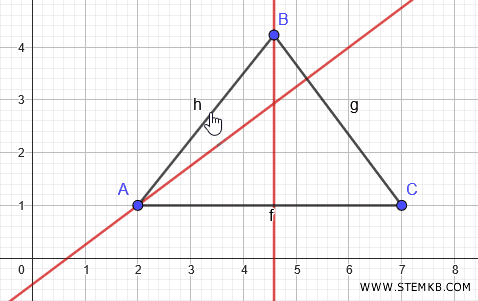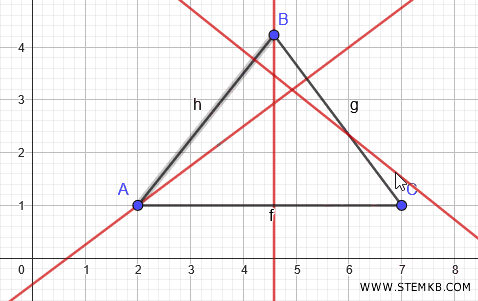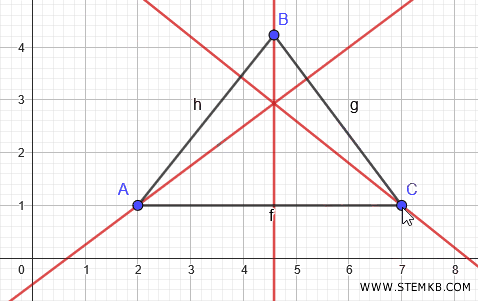
Le tre altezze si intersecano in un punto. Questo punto è l'ortocentro del triangolo.

Ora seleziona lo strumento Intersezione.

 

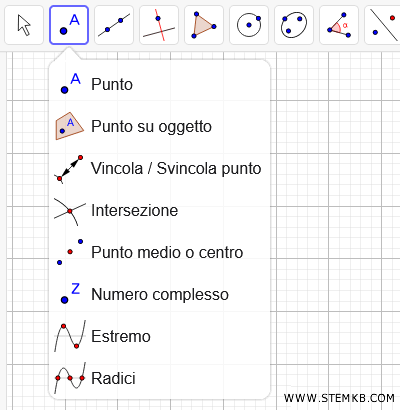
Poi clicca sul punto di intersezione delle tre altezze.

Questo punto è l'ortocentro del triangolo.

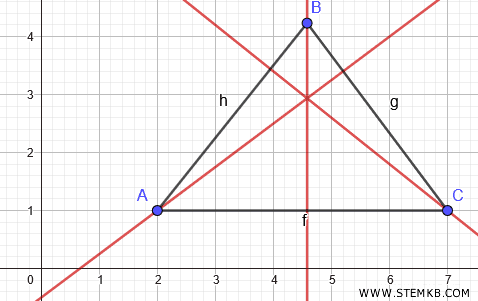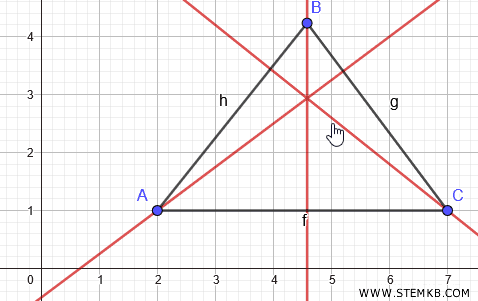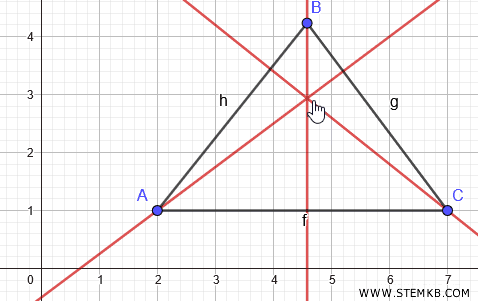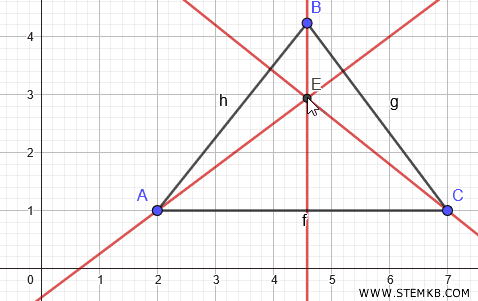
Se adesso selezioni uno dei vertici del triangolo e cominci a spostarlo, puoi vedere come cambia l'ortocentro al variare degli angoli del triangolo.

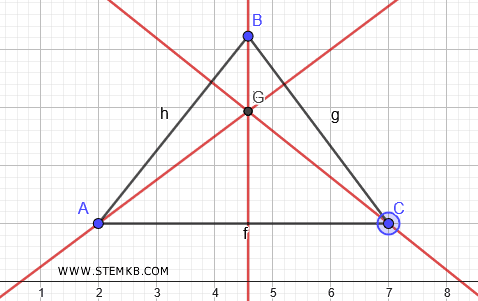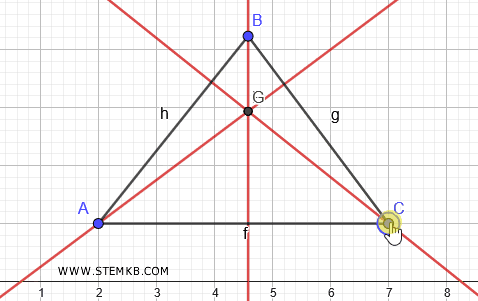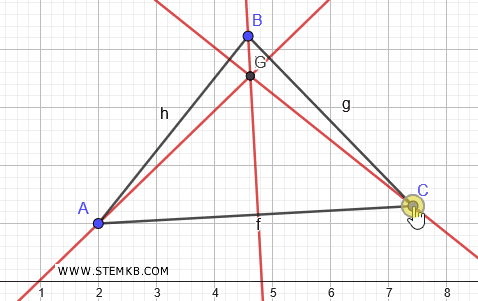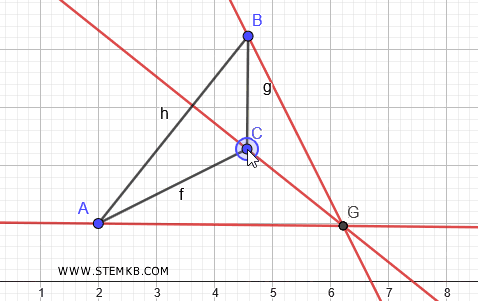
Nei triangoli acutangolo l'ortocentro è all'interno del triangolo.

Nel caso dei triangoli ottusangolo, invece, l'ortocentro si sposta all'esterno del triangolo.